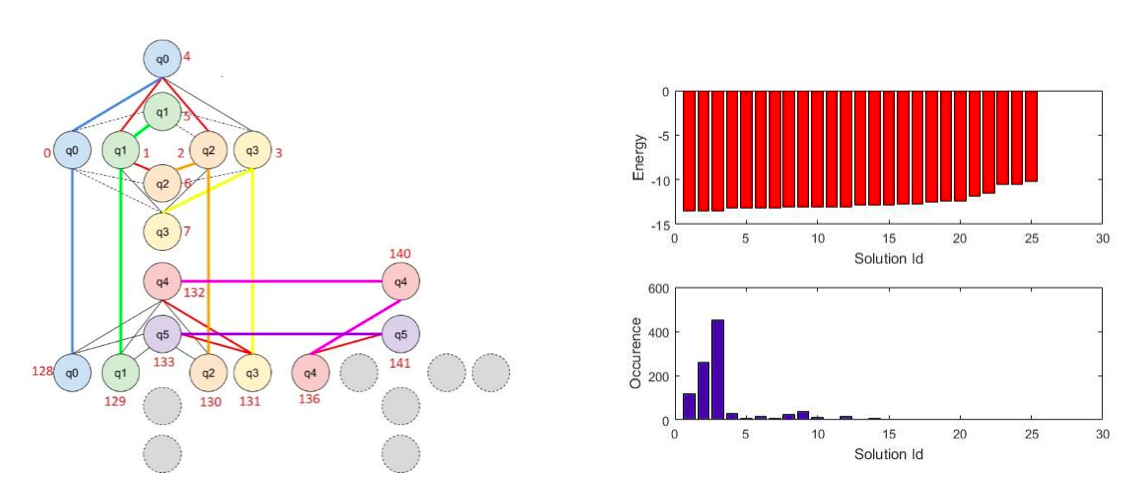
*Keterangan gambar: Sambungan antar qubit di dalam komputer kuantum D-Wave 2000Q untuk menemukan matriks Hadamard 2x2 dan sebaran energi hasil eksekusi dari program. (Foto: Prof. Andriyan)

Dijelaskan Prof. Andriyan, Matriks Hadamard adalah suatu matriks ortogonal dengan elemen -1 dan +1. Sebarang pasangan vektor kolom atau pasangan vektor baris dari matriks tersebut saling tegak-lurus. Matriks ini ditemukan oleh J.J. Sylvester dan selanjutnya dikembangkan oleh J. Hadamard dari Perancis.

Menemukan satu matriks Hadamard di antara seluruh matriks biner yang ada, dapat dikategorikan sebagai hard problem. Peluang menemukan matriks yang demikian akan mengecil secara eksponensial seiring dengan kuadrat ukuran matriks. Algoritma kuantum yang telah dibuat dan diimplementasikan sebagai program di dalam komputer kuantum D-Wave 2000Q mampu mengatasi permasalahan tersebut. Hasil penelitian ini pun telah dipublikasikan dalam jurnal Nature’s Scientific Reports yang terbit pada awal bulan Oktober 2019.

“Matriks Hadamard dipakai dalam berbagai aplikasi, antara lain untuk kode pengoreksi kesalahan (ECC-Error Correcting Code) atau kode penebar dalam sistem komunikasi CDMA (Code Division Multiple Access). Sebagai ECC, kode Hadamard dimanfaatkan dalam pengiriman citra planet Mars oleh wahana antariksa Mariner 9. Dalam sistem CDMA, sifat ortogonal dari matriks ini dimanfaatkan agar sinyal antar pengguna sistem tidak saling mengganggu,” ungkapnya.

Lebih lanjut, Prof. Andriyan menerangkan bahwa secara prinsip, suatu matriks Hadamard dapat dicari dengan mencoba semua kombinasi -1 dan 1 pada semua elemen, lalu memeriksa ortogonalitas dari matriks tersebut. Namun demikian langkah yang diperlukan akan menjadi sangat panjang sehingga waktu eksekusinya sangat lama.

“Untuk menemukan satu matriks berukuran MxM, diperlukan langkah perhitungan sebanyak 2^(MxM) sehingga masuk kategori hard problem. Komputasi kuantum dapat mengatasi hal ini karena memiliki kemampuan merepresentasikan elemen -1 dan 1 (atau 0 dan 1) sekaligus sebagai superposisi,” terang guru besar pada Kelompok Keahlian Teknik Telekomunikasi itu. 

Menurutnya, metode yang diajukan ini dapat menemukan matriks Hadamard sebarang ukuran dengan pola 4kx4k, jika conjecture Hadamard benar dan komputer kuantum yang dipakai memiliki jumlah qubit yang cukup. Saat ini, komputer kuantum yang ada baru berhasil merealisasikan algoritma pencarian matriks Hadamard 2x2 dan 4x4.

“Dengan semakin pesatnya kemajuan teknologi komputer kuantum, kemampuan dan jumlah qubits yang dibuat juga semakin meningkat. Diharapkan algoritma ini kelak dapat dipakai sebagai alat benchmarking komputer kuantum,” jelasnya.