GNN or graph neural network itself is one of the deep learning architectures used to solve machine learning problems in graphic data. According to Prof. Martin, gnn can be reviewed as a common form of convolutional neural network (CNN) of lattice structures (pixels in images) that tend to be 'rigid' into more flexible data but still structured.

"The real difference between GNN (graph neural network) and 'traditional' artificial intelligence is that the basic 'traditional' artificial intelligence is still on logic."

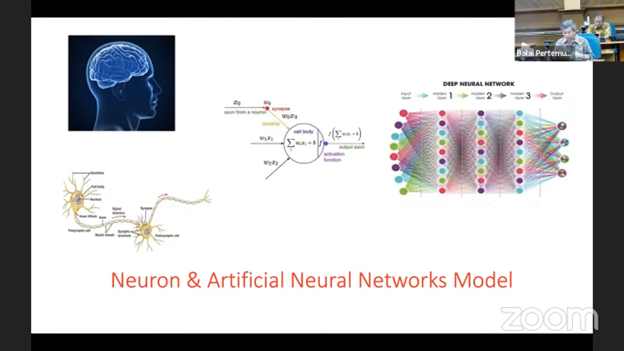
GNN and its functions.

He explained that the data in GNN is in the form of a real number vector with an information exchange flow that has no specific rules or turns. The initial vector then undergoes aggregation after receiving data from its nearest point.

After the aggregation process, it is necessary to decide what things you want to be computing. There are two options in GNN, namely, to compute node-level function or graph-level function. GNN itself has a predetermined number of layers, with each layer having a different aggregation function.

"The dots, as shown in the image, will send data and simultaneously receive data from the nearest point. After exchanging information, each of these points updates the data they have," he said.

The question thrown by Martin Grohe is, what if we only have one aggregation function or one combination function? This question is then answered right after, in the explanation about recurrent GNN. Recurrent GNN is when one aggregation function is applied continuously for as long as we want. This is possible because the number of iterations is not specified.

"The size of graph used as input or the evolution of sequence that occurred is the one that determines the number of iterations," he explained. This evolution, for example, is when the iteration stops as the sequence begins to converge at some point.

Weisfeiler-Leman Algorithm

The discussion on the Weisfeiler-Leman algorithm opens with an introduction to the color refinement algorithm that iteratively computes the dots on a graph with color.

He said the two graphs could be distinguished using this algorithm. The relationship between GNN and the color refinement algorithm is an abstraction of what GNN does.

In conclusion, at the end of his presentation, Prof. Martin Grohe emphasized that GNN is a very flexible learning architecture and can adapt to logical formalism, for example, to adapt to constraint satisfaction problems (CSPs) that provide a common framework for combinatorial search problems.

Reporter: Athira Syifa PS (Teknologi Pascapanen, 2019)
Translator: Aghisna Syifa R (Biologi, 2020)